Introduction

This story begins the day after I got home after giving a talk at the wonderful DevFest Siberia. Shortly after my weekly fix of Westworld, a strange nagging feeling appeared — like the one you get from unpaid bills, a postcard that you forgot to send, or a particularly nasty API endpoint that you were supposed to refactor a year ago but then, well, I mean, it works, right?

Then I remembered. I emptied out my suitcase and found the cause of the uneasiness: two stickers with goofy cartoon gophers on them. The first one was really enjoying their beer. The other one has just put on a wizard hat — possibly matched with a robe. They were looking right into my eyes.

The first rule of IT conferences is simple: if someone gives you a sticker, you must try the product. Everyone knows that. People place great trust in you by handing out these colorful pieces of adhesive paper, and doing nothing about my new gopher friends would be outright criminal. I had to write something in Go.

An Enigma emulator is a reasonably solid choice for getting a first impression of a programming language: it is fundamentally simple, but nuanced enough to get familiar with at least a few language quirks by the time it is done. I have set aside a couple afternoons and a weekend — and it turned out to be enough to get from zero to a fully documented reusable Enigma library with a CLI app.

Go is surprisingly easy to learn on a basic level — as long as you have some programming experience and, ideally, know a thing or two about pointers. Enigma, on the other hand, is a bit more challenging. Mainly, I will try to describe how Enigma works, and then provide the Go code implementing the parts.

What if you know nothing about Go at all? What if Enigma for you is a strange box where magic happens (and also Benedict Cumberbatch is somehow involved)? Well, that is just awesome — it means I have a chance to get you curious about both of these things!

The full library — along with a CLI app that is not covered in this post — is available at github.com/emedvedev/enigma. Naturally, there is a GoDoc page as well.

Let’s begin!

Enigma 101

There are quite a few excellent articles and even entire websites explaining how Enigma works in great detail (Tony Sale’s is probably my favorite), so I will only give a very basic explanation before we move to the coding, leaving nuances to serious Enigma-focused publications.

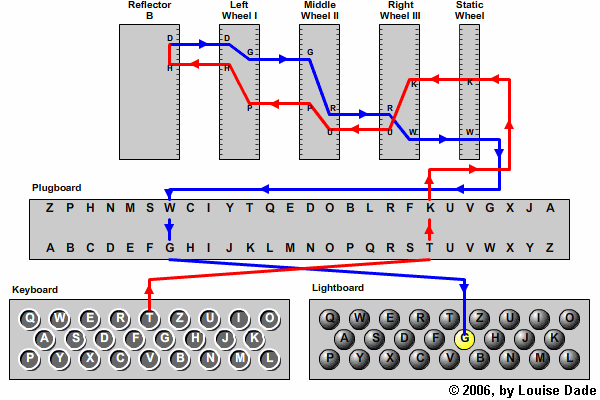
Enigma is a rotor-based machine: each letter is encoded by an electric signal going through a number of rotors (they can be seen on the picture), with each rotor performing a letter substitution. Most importantly, one or more rotors would move before encoding, changing the substitution alphabet with every subsequent character.

After the first pass through the rotors, the signal goes through a reflector: it performs one more substitution and sends the signal back through the rotors, this time in reverse order. You can see the reflector to the left of the rotors, marked with “B” to denote its wiring (several different reflectors were in use).

To scramble the message even further, a plugboard is used to make letter pairs that will be swapped both before and after encoding. You can see the connected pairs on the image above (takes some effort unless you were really into “help the rabbit get to carrots” puzzles as a kid): some of them are IO, PT, EW, and RQ, so if your input is “GOPHER”, it is transformed to “GITHWQ” before being encoded. The same swap is applied to the encoded letters right before output.

A wiring diagram should make things clearer:

If things are still unclear, you can practice on a papercraft Enigma compatible with a 165g Pringles tube.

Now that we know the basics, we can start with some boilerplate code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

package enigma

import "bytes"

type Enigma struct {
	// We'll get to those later.
	Reflector Reflector
	Plugboard Plugboard
	Rotors    Rotors
}

func (e *Enigma) EncodeChar(letter byte) byte {
	// This is where magic happens! Wow!
	// 1. Move the rotors.
	// 2. Swap the input character if there is a plugboard pair.
	// 3. Step into each rotor (right to left).
	// 4. Step into the reflector.
	// 5. Step into each rotor (left to right).
	// 6. Swap the result if there is a plugboard pair.
	// 7. Return the result.
}

func (e *Enigma) EncodeString(text string) string {
	var result bytes.Buffer
	for i := range text {
		result.WriteByte(e.EncodeChar(text[i]))
	}
	return result.String()
}

Footnote: using runes would be more semantically correct than bytes, I guess, but we only encrypt ASCII, so it’s fine. The real reason behind using bytes is that they’ve turned out to work a little faster when I had to run eleven million Enigma configurations.

Initial configuration

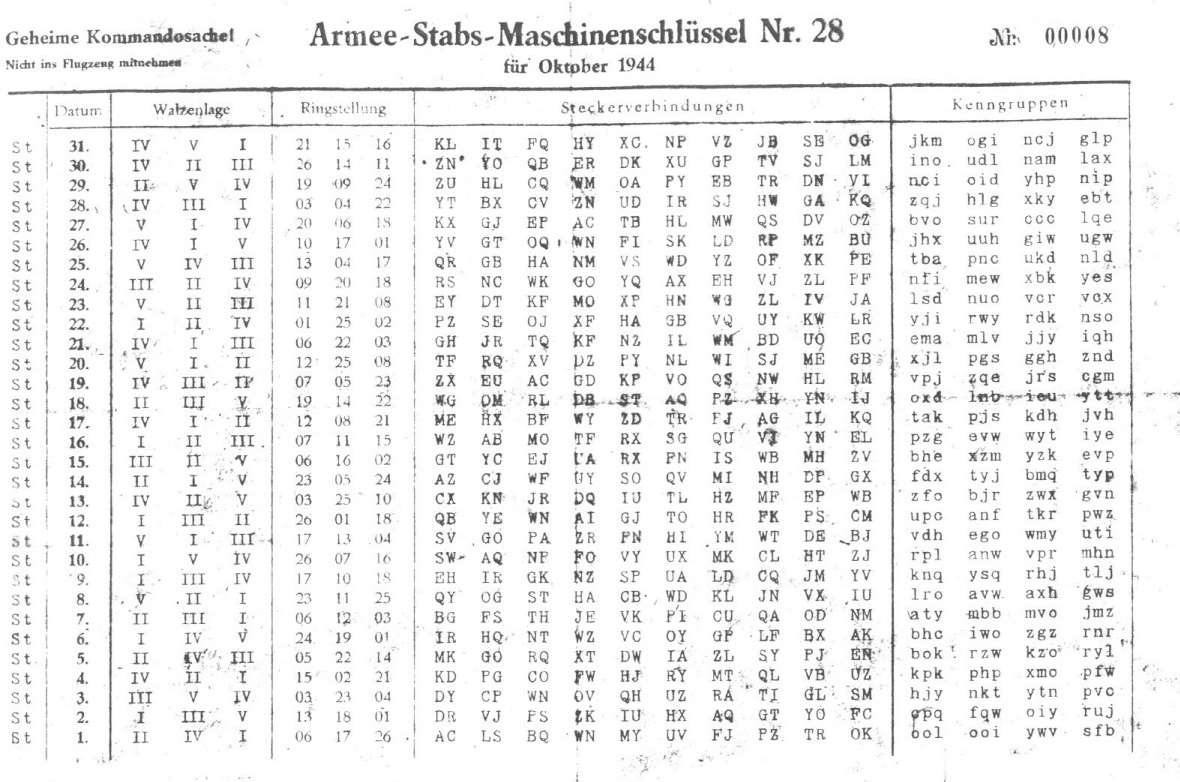
To decrypt an Enigma-encoded message, you must know the configuration that was used to encrypt it. Enigma configurations were distributed on key sheets, like the one above, and changed daily. For obvious reasons, key sheets were considered top secret information and highly protected. Only the officers were trusted with them, and they were often required to configure the machines personally and lock the insides so that even the operators did not know the settings.

Here is what a daily entry consisted of:

• “IV V I” (Walzenlage) is the rotors order. Eight rotors with different wiring were supplied with the machines, the three rotors in use (and their order) would change every day.
• “21 15 16” (Ringstellung) is the ring setting. Every rotor had a configurable “ring” that would shift the encryption alphabet by a given amount (1 to 26).

• “KL IT … SE OG” (Steckerverbindungen) are the plugboard pairs, already described in a previous section.

• “jkm … glp” (Kenngruppen) are the key groups: they were used to communicate the starting positions of the rotors. The procedure for using keys has nothing to do with the Enigma machine itself — the operators did it — so the only part that matters is being able to set the initial rotor positions.

Now that we know the settings that were used, let’s take a look at the constructor:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

type RotorConfig struct {
	ID    string
	Start byte
	Ring  int
}

func NewEnigma(rotorConfiguration []RotorConfig, refID string, plugs []string) *Enigma {
	// More magic!
	// 1. Get the rotor models by their UIDs ("I" to "VIII") and load the parameters.
	// 2. Create a plugboard mapping from the supplied pairs.
	// 3. Get the reflector by its UID.
	// 4. Return the new Enigma instance.
}

I know there is still a lot of magic and boilerplates, but bear with me: including the implementation details would be too confusing at this point. Think of it as a progressive JPEG kind of thing.

A lot of real code in the next section though!

Rotors

Rotors were the heart of the Enigma machines. Essentially, each rotor performs a simple letter substitution according to its internal wiring:

1
2
3

ABCDEFGHIJKLMNOPQRSTUVWXYZ
||||||||||||||||||||||||||
EKMFLGDQVZNTOWYHXUSPAIBRCJ

When the signal goes towards a reflector (from right to left), “A” is encoded to “E”, and then the signal goes on to the next rotor. After the reflector, the signal gets reversed: “A” would be encrypted to “U”.

As mentioned before, the rotor parts are movable. When the rotor is moved, the substitution table gets offset:

1
2
3

BCDEFGHIJKLMNOPQRSTUVWXYZA
||||||||||||||||||||||||||
EKMFLGDQVZNTOWYHXUSPAIBRCJ

Now it is “B”, not “A”, that encodes to “E”.

The operator could set the starting position for each rotor manually, and just like every other configuration parameter, starting positions were changed daily during the war.

A ring setting (set through a small ring on the rotor) would add a fixed offset: with the starting position “B” and the ring setting 4, the table would have an offset of three positions.

Another important part is stepping — moving rules for the rotors. We will get to it after we are done with the rest of the parts, but for now it is important to know that rotors had notches next to one of the letters (rotors V through VIII had two), and when Enigma “encountered” that notch, the rotor on the left was shifted. On the picture above, the rotor on the left has a visible notch at H, and the rotor on the right has a notch at U.

Let’s create a simple type for the rotors:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

type Rotor struct {
	ID          string
	StraightSeq [26]int
	ReverseSeq  [26]int
	Turnover    []int

	Offset int
	Ring   int
}

type Rotors []Rotor

Note that letter sequences are [26]int: inside the library, we are going to be working with int values for letters (0 for 'A', 25 for 'Z'), rather than bytes or runes. We do not care about the characters themselves when performing the encoding — their position and offset matter much more — so we are saving ourselves from a bunch of extra rune/int conversions during the encoding process.

We still have to perform the conversion in constructors, so here are the two helper functions:

1
2
3
4
5
6
7

func CharToIndex(char byte) int {
	return int(char - 'A')
}

func IndexToChar(index int) byte {
	return byte('A' + index)
}

Curiously, the reason something like this works is that rune is an alias for int32 in Go; there is a useful post in The Go Blog on characters, bytes, and strings that I would recommend.

Let’s define a constructor and create the eight preset rotors that were in use at the time. A helper method for the rotor list to get rotors by ID is included (although making Rotors a map instead of a list is also an option):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

func NewRotor(mapping string, id string, turnovers string) *Rotor {
	r := &Rotor{ID: id, Offset: 0, Ring: 0}
	r.Turnover = make([]int, len(turnovers))
	for i := range turnovers {
		r.Turnover[i] = CharToIndex(turnovers[i])
	}
	for i, letter := range mapping {
		index := CharToIndex(byte(letter))
		r.StraightSeq[i] = index
		r.ReverseSeq[index] = i
	}
	return r
}

func (rs *Rotors) GetByID(id string) *Rotor {
	for _, rotor := range *rs {
		if rotor.ID == id {
			return &rotor
		}
	}
	return nil
}

var HistoricRotors = Rotors{
	*NewRotor("EKMFLGDQVZNTOWYHXUSPAIBRCJ", "I", "Q"),
	*NewRotor("AJDKSIRUXBLHWTMCQGZNPYFVOE", "II", "E"),
	*NewRotor("BDFHJLCPRTXVZNYEIWGAKMUSQO", "III", "V"),
	*NewRotor("ESOVPZJAYQUIRHXLNFTGKDCMWB", "IV", "J"),
	*NewRotor("VZBRGITYUPSDNHLXAWMJQOFECK", "V", "Z"),
	*NewRotor("JPGVOUMFYQBENHZRDKASXLICTW", "VI", "ZM"),
	*NewRotor("NZJHGRCXMYSWBOUFAIVLPEKQDT", "VII", "ZM"),
	*NewRotor("FKQHTLXOCBJSPDZRAMEWNIUYGV", "VIII", "ZM"),
}

Finally, the method performing the substitution. We need to account for the current position and the ring settings — this is one of the examples where thinking of letters as their indexes helps us avoid unnecessary conversions:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

func (r *Rotor) Step(letter int, invert bool) int {
	letter = (letter - r.Ring + r.Offset + 26) % 26
	if invert {
		letter = r.ReverseSeq[letter]
	} else {
		letter = r.StraightSeq[letter]
	}
	letter = (letter + r.Ring - r.Offset + 26) % 26
	return letter
}

Another footnote: I tried to make my Go code as idiomatic as possible by applying the best method I know, which is looking up my stupid questions on Stack Overflow and copying the answers if they are written by Dave Cheney. However, despite this tremendous effort, there are bound to be some ugly parts — please do point them out.

Reflectors

A reflector (also known as a reversing drum or UKW) performs a simple letter swap — “M” to “N”, “N” to “M” — with the letter pairs hardwired. A configurable reflector, UKW-D, has been introduced in 1944, but was rare enough to ignore in our emulator.

Same as with rotors, we’ll store a [26]int mapping, but since the letters are swapped in pairs, we can do without the reverse map. A common representation of a reflector is a mapping string (YRUHQSLDPXNGOKMIEBFZCWVJAT), so we’ll make the constructor accept it:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

type Reflector struct {
	ID       string
	Sequence [26]int
}

func NewReflector(mapping string, id string) *Reflector {
	var seq [26]int
	for i, value := range mapping {
		seq[i] = ToInt(byte(value))
	}
	return &Reflector{id, seq}
}

The Reflectors type for the list and the GetByID method for reflectors are nearly identical to those of the rotors, so I will not provide them here.

Lastly, we will need a preset. Two reflectors, B and C (with C being rare and almost unused), were used in the M3 machines:

1
2
3
4

var HistoricReflectors = Reflectors{
	*NewReflector("YRUHQSLDPXNGOKMIEBFZCWVJAT", "B"),
	*NewReflector("FVPJIAOYEDRZXWGCTKUQSBNMHL", "C"),
}

Reflectors provided symmetry to Enigma machines: a path from “A” to “Z” would be the same as the path from “Z” to “A”. Because of that, encryption and decryption were essentially the same. However, because of reflectors, letters could never be encoded into themselves — a serious flaw that was heavily exploited by codebreakers.

Plugboard

We’re almost ready to encode all the things! Only the plugboard is missing, and since a simple letter swap is all it does, we can define it as [26]int and map unspecified letters to themselves in the constructor:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

type Plugboard [26]int

func NewPlugboard(pairs []string) *Plugboard {
	p := Plugboard{}
	for i := 0; i < 26; i++ {
		p[i] = i
	}
	for _, pair := range pairs {
		if len(pair) > 0 {
			var intFirst = ToInt(pair[0])
			var intSecond = ToInt(pair[1])
			p[intFirst] = intSecond
			p[intSecond] = intFirst
		}
	}
	return &p
}

That is it. Really simple.

Rotor stepping

There is only one thing left to do before we can stuff that boilerplate method in the Enigma type with code: learn how to move the rotors.

The rules are as follows:

1. Rotors move on a keypress, but before a character is encoded.
2. The right rotor always moves.
3. If the rotor moves from a notch position, a rotor on its left moves.
4. If the middle rotor advances the left rotor, the middle rotor moves again at the next step.

The last rule is called double stepping, and it is, admittedly, hella confusing. The reason is that it was not the intended design, but rather an engineering flaw. Since most Enigma machines share this property — including the M3 — we have to emulate it as well.

These principles are not hard to describe as code — and we will create a couple more helper methods to keep the Enigma method itself lightweight and readable:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

func (r *Rotor) move(offset int) {
	r.Offset = (r.Offset + offset) % 26
}

func (r *Rotor) ShouldTurnOver() bool {
	for _, turnover := range r.Turnover {
		if r.Offset == turnover {
			return true
		}
	}
	return false
}

func (e *Enigma) moveRotors() {
	var (
		rotorLen            = len(e.Rotors)
		farRight            = e.Rotors[rotorLen-1]
		farRightTurnover    = farRight.ShouldTurnOver()
		secondRight         = e.Rotors[rotorLen-2]
		secondRightTurnover = secondRight.ShouldTurnOver()
		thirdRight          = e.Rotors[rotorLen-3]
	)
	if secondRightTurnover {
		if !farRightTurnover {
			secondRight.move(1)
		}
		thirdRight.move(1)
	}
	if farRightTurnover {
		secondRight.move(1)
	}
	farRight.move(1)
}

Nevermind the variable naming: secondRight and thirdRight could be middle and left on M3, but the library also supports M4 that has four rotors, so it would be incorrect.

Congratulations! Everything inside our Enigma is working as it is supposed to.

Wiring it all together

The Enigma constructor and the boilerplate encodeChar method we have created at the very beginning are all that is still left unfinished, and now we have everything we need to complete the machine:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

func (e *Enigma) EncodeChar(letter byte) byte {
	// This is where magic happens! Wow!

	// 1. Move the rotors.
	e.moveRotors()

	// 2. Swap the input character if there is a plugboard pair.
	letterIndex := CharToIndex(letter)
	letterIndex = e.Plugboard[letterIndex]

	// 3. Step into each rotor (right to left).
	for i := len(e.Rotors) - 1; i >= 0; i-- {
		letterIndex = e.Rotors[i].Step(letterIndex, false)
	}

	// 4. Step into the reflector.
	letterIndex = e.Reflector.Sequence[letterIndex]

	// 5. Step into each rotor (left to right).
	for i := 0; i < len(e.Rotors); i++ {
		letterIndex = e.Rotors[i].Step(letterIndex, true)
	}

	// 6. Swap the result if there is a plugboard pair.
	letterIndex = e.Plugboard[letterIndex]
	letter = IndexToChar(letterIndex)

	// 7. Return the result.
	return letter
}

func NewEnigma(rotorConfiguration []RotorConfig, refID string, plugs []string) *Enigma {
	// More magic!

	// 1. Get the rotor models by their UIDs ("I" to "VIII") and load the parameters.

	// 2. Create a plugboard mapping from the supplied pairs.
	// 3. Get the reflector by its UID.
	// 4. Return the new Enigma instance.
}

Magic! Let’s import the library and test it:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

package main

import (
	"fmt"

	"github.com/emedvedev/enigma"
)

func main() {
	e := enigma.NewEnigma(
		[]enigma.RotorConfig{
			enigma.RotorConfig{ID: "III", Start: 'A', Ring: 1},
			enigma.RotorConfig{ID: "II", Start: 'B', Ring: 1},
			enigma.RotorConfig{ID: "IV", Start: 'C', Ring: 1},
		},
		"B",
		[]string{"AB", "CD", "EF"},
	)
	plaintext := "HELLOWORLD"
	ciphertext := e.EncodeString(plaintext)

	fmt.Printf("%s is encoded as %s\n", plaintext, ciphertext)

	e2 := enigma.NewEnigma(
		[]enigma.RotorConfig{
			enigma.RotorConfig{ID: "III", Start: 'A', Ring: 1},
			enigma.RotorConfig{ID: "II", Start: 'B', Ring: 1},
			enigma.RotorConfig{ID: "IV", Start: 'C', Ring: 1},
		},
		"B",
		[]string{"AB", "CD", "EF"},
	)

	plaintext2 := ciphertext
	ciphertext2 := e2.EncodeString(plaintext2)

	fmt.Printf("%s is encoded as %s\n", ciphertext, ciphertext2)
}

1
2

HELLOWORLD is encoded as YGMGTTPJNJ
YGMGTTPJNJ is encoded as HELLOWORLD

It’s alive! We are officially done.

Now you can try encrypting and decrypting messages with other online emulators for verification: for example, Universal Enigma supports a wide range of Enigma models and settings, and is overall amazing.

You could also use a real Enigma machine, of course: after all, there is nothing better than original, and it will only run you down a meager sum of $365,000. You can’t afford not to buy it!

And of course, I just cannot recommend the Pringles Enigma enough as a cheaper and a more functional alternative. You can eat and encode with the same device! This is the future, right here.

And finally, a simple exercise for the reader:

1
2
3

III II IV | 5 10 18 | A A A | AE DQ RC VB MT OG PF YL JW IZ

PJHLFULLUECCPFLCIVPMFDAWJCWANLVXAIXFHMACNLVNCSXOIXFUTGWXSRULRTXPOIPUINCYOGWKGZAZDMVPOUIDCRSCHSZCNTFJADAVIKOGSYAJGAFNELPOMBMTXEXVAREVMSBNHLJFEGZ